Star and Delta Configurations

Star and Delta configurations occur frequently in resistor networks and it can be useful to change from one to the other as part of the process of calculating the overall resistance. They are also used extensively in three phase electrical circuits but that will not be covered here.

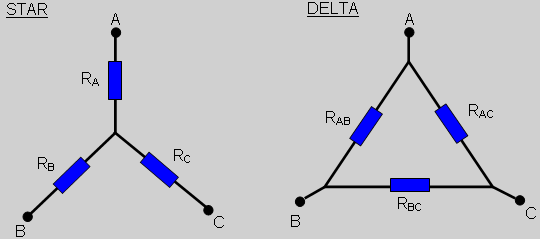
The Star network is also known as the T or Y configuration and the Delta network is also known as the triangle (Δ) or pi (Π) configuration.

Delta to Star Transformation

First eliminate the connection C considering it to by open circuit.
For the star configuration this makes the resistance between A and B equal to R_A + R_B.
For the delta configuration the resistance between A and B is equal to R_AB in parallel with R_BC + R_AC which is equal to R_AB(R_BC + R_AC)/(R_AB + R_BC + R_AC).

As these networks must always be equivalent: R_A + R_B = R_AB(R_BC + R_AC)/(R_AB + R_BC + R_AC).
Similarly for B open circuit: R_A + R_C = R_AC(R_AB + R_BC)/(R_AB + R_BC + R_AC).
Finally for A open circuit: R_B + R_C = R_BC(R_AB + R_AC)/(R_AB + R_BC + R_AC).

From these three independent equations after some manipulation the following is obtained:

R_A = R_ABR_AC/(R_AB + R_BC + R_AC)
R_B = R_ABR_BC/(R_AB + R_BC + R_AC)
R_C = R_BCR_AC/(R_AB + R_BC + R_AC)

Star to Delta Transformation

R_AB = R_A + R_B + R_AR_B/R_C
R_BC = R_B + R_C + R_BR_C/R_A
R_AC = R_A + R_C + R_AR_C/R_B